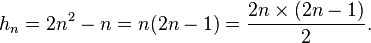La espiral de Teodoro

La espiral que aparece arriba se conoce con el nombre de "espiral de Teodoro" y constituye un método para construir geométricamente los segmentos de longitud . El segmento horizontal inicial es un segmento de longitud igual a la unidad, igual que los segmentos perpendiculares que se van añadiendo. Del teorema de Pitágoras se deduce que la longitud de los segmentos radiales es la indicada: . No hay constancia de que Teodoro de Cirene dibujara la espiral pero sí se sabe que demostró la irracionalidad de los segmentos de longitudes y la espiral, debido a su simplicidad y belleza, aparece reproducida en numerosos libros de texto. Aquí raíz cuadrada de 3 significa longitud del lado del cuadrado de área 3 e irracionalidad significa inconmensurabilidad de esa longitud del lado con la del lado de un cuadrado de área unidad (inconmensurabilidad = inexistencia de un segmento que sirva de medida común a ambos segmentos). Se desconoce la razón por la que no generalizó el resultado a números mayores y por la que se detuvo en el caso 17. Algunos autores han conjeturado que no quiso continuar porque significaba dar otra vuelta y superponer los dibujos (Paul Nahin: "An Imaginary Tale: The history of ").

permutaciones en curculo

si uno de ellos se le deja siempre en un mismo lugar por ejemplo a 1 seria la permutacion de los restantes Permutación de n elmentos realizaremos las permutacuiones de n-1 elementos N ELEMENTOS = ( N - 1 )! POR EJEMPLO EN LA IMAGEN DE ARRIBA HAY 6 ELEMENTOS , REALIZARIAMOS LAS PERMUTACIONE DE 5! = 120

canción del numero de oro

DIAGRAMA DE ÀRBOL.

Un diagrama de árbol es una herramienta que se utiliza para determinar todos los posibles resultados de un experimento aleatorio.


En el cálculo de la probabilidad se requiere conocer el número de elementos que forman parte del espacio muestral, estos se pueden determinar con la construcción del diagrama de árbol.


El diagrama de árbol es una representación gráfica de los posibles resultados del experimento, el cual consta una serie de pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo. Se utiliza en los problemas de conteo y probabilidad.

Aguja de Buffon

La aguja de Buffon es un clásico problema de probabilidad geométrica, de inmediata realización práctica y cuyo interés radica en que es un método sencillo para ir aproximando el valor del número π a partir de sucesivos intentos. Fue planteado por el naturalista francés Buffon en 1733 y reproducido por él mismo ya resuelto en 1777 . Se trata de lanzar una aguja sobre un papel en el que se han trazado rectas paralelas distanciadas entre sí de manera uniforme. Se puede demostrar que si la distancia entre las rectas es igual a la longitud de la aguja, la probabilidad de que la aguja cruce alguna de las líneas es 2 / π.

П = 2N/A

Si la aguja es más corta que la distancia entre las rectas la probabilidad disminuye proporcionalmente al cociente entre la longitud de la aguja y la distancia entre las rectas, tomando el valor 2L / (Dπ) donde L es la longitud de la aguja y D la interdistancia entre las rectas.

П = 2NL/AD

La tercera situación, en que la longitud de la aguja es mayor que la distancia entre las rectas lleva a un resultado bastante más complicado.

Una generalización obvia de este problema es el problema de la Aguja de Buffon-Laplace, donde la aguja, en vez de lanzarse sobre un papel rayado, se lanza sobre una cuadrícula. Se llama de Buffon-Laplace pues aunque Buffon lo resolvió también en 1777, su solución contenía un error. Fue corregido por Laplace en 1812.

curiosidades sobre pi ( П )

Curiosidades

En 1983, Rajan Mahadevan fue capaz de recitar de memoria 31.811 decimales de pi.

Los pies de un elefante tienen forma circular. Multiplica el diámetro de su pie por 2П y el resultado obtenido es la altura del elefante (de los pies a la espalda).

Si quisiéramos escribir en línea recta los 200.000 millones de decimales de pi calculados por Kanada y Takahasi en 1999, el papel necesario tendría una longitud tal, que podría dar una vuelta a la circunferencia de la Tierra. (Fuente: Times New Roman; Tamaño: 12; 5 dígitos en cada centímetro)

Con sólo unos 40 decimales del número pi se podría calcular la longitud de una circunferencia que abarcara a todo el universo visible, con un error menor que el radio de un átomo de hidrógeno.

Si tomamos dos números enteros positivos al azar, la probabilidad de que sean coprimos (no tengan factores comunes) es 6 /pi2.





Si en este poema cuentas las letras de cada palabra tendrás las primeras veinte cifras de :

Soy y seré a todos definible,
mi nombre tengo que daros,
cociente diametral siempre inmedible
soy de los redondos aros.

Esta otra frase nos da las diez primeras cifras decimales de :

Con 1 hilo y 5 mariposas
se pueden hacer mil cosas.

El Número Pi
(Poema de Wislawa Szymborska)

Digno de admiración es el número Pi
tres coma catorce,
Todas sus siguientes cifras también son iniciales,
quince noventa y dos porque nunca termina.
No se deja abarcar sesenta y cinco treinta y cinco con la mirada,
ochenta y nueve con los cálculos
setenta y nueve con la imaginación
y ni siquiera treinta y dos treinta y ocho con una broma o sea comparación
cuarenta y seis con nada
veintiséis cuarenta y tres en el mundo.
La serpiente más larga de la tierra después de muchos metros se acaba.
Lo mismo hacen aunque un poco después las serpientes de las fábulas.
La comparsa de cifras que forma el número Pi
no se detiene en el borde de una hoja,
es capaz de continuar por la mesa, el aire,
la pared, la hoja de un árbol, un nido, las nubes, y así hasta el cielo,
a través de toda esa hinchazón e inconmensurabilidad celestiales.
Oh, qué corto, francamente rabicorto es el cometa.
¡En cualquier espacio se curva el débil rayo de una estrella!
Y aquí dos treinta y uno cincuenta y tres diecinueve
mi número de teléfono el número de tus zapatos
el año mil novecientos setenta y tres piso sexto
el número de habitantes sesenta y cinco céntimos
centímetros de cadera dos dedos charada y mensaje cifrado,
en la cual ruiseñor que vas a Francia
y se ruega mantener la calma
y también pasarán la tierra y el cielo,
pero no el número Pi, de eso ni hablar,
seguirá sin cesar con un cinco en bastante buen estado,
y un ocho, pero nunca uno cualquiera,
y un siete, que nunca será el último,
y metiéndole prisa, eso sí, metiéndole prisa a la perezosa eternidad para que continúe.

CANCIÓN SOBRE PI

nº poligonales

Nº TRIANGULAR
Un número triangular es aquel que puede recomponerse en la forma de un triángulo equilátero (por convención, el primer número triangular es el 1). Los números triangulares, junto con otros números figurados, fueron objeto de estudio por Pitágoras y losPitagóricos, quienes consideraban sagrado el 10 escrito en forma triangular, y al que llamaban Tetraktys.

NºCUADRADO

Un número cuadrado perfecto en matemáticas, o un número cuadrado, es un número entero que es el cuadrado de algún otro; dicho de otro modo, un número cuya raíz cuadrada es un número entero.

Por ejemplo, 9 es un número cuadrado perfecto ya que puede ser escrito como 3 × 3.

32 = 9

Un número entero positivo que no tiene divisores cuadrados (excepto el 1) se denomina número libre de cuadrados.

Nº PENTAGONAL

Un número pentagonal es un número figurado que extiende el concepto de número triangular y cuadrado al pentágono, pero, a diferencia de los dos primeros, los patrones utilizados en la construcción de los números pentagonales no son simétricamente rotacionales.

Nº HEXAGONAL

Un número hexagonal es un número poligonal que se puede representar en forma de hexágono.

La fórmula para un número hexagonal n es:

Bienvenidos a mi blog.

Hola ,

Este es mi blog para la asignatura  de profundizacion de matemáticas , no puedo prometer y no prometo que pondre cosas interesantes.

Sonia.